线性变换中有的将空间向外拉伸，有的则将空间向内挤压，所以变换究竟对空间有多少拉伸或挤压？如何测量和表示？
线性变换的行列式：给定区域面积（体积）增大或减小的比例
1. 矩阵的行列式（2D）
前已述过，矩阵代表着一种线性变换，是对空间的一种操纵。在二维空间中，$det(A)$的值即为给定区域面积缩放比例。
$det(A)=0$
行列式为零，意味着将一个二维空间压缩为一条线（面积变为零）。故只需要检验一个矩阵的行列式是否为零，就能知道这个矩阵所代表的变换是否将空间压缩到更小的维度上。
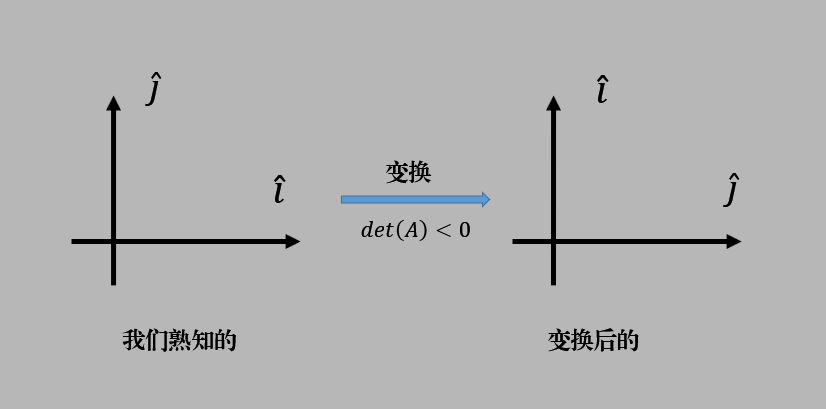
$det(A)<0$
显然，我们能想到行列式大于零的情况，其实行列式也存在是负值的情况的。这里就是一个定向改变的问题。
基向量 $\hat{i},\hat{j}$ 的定向改变与行列式为负的关系
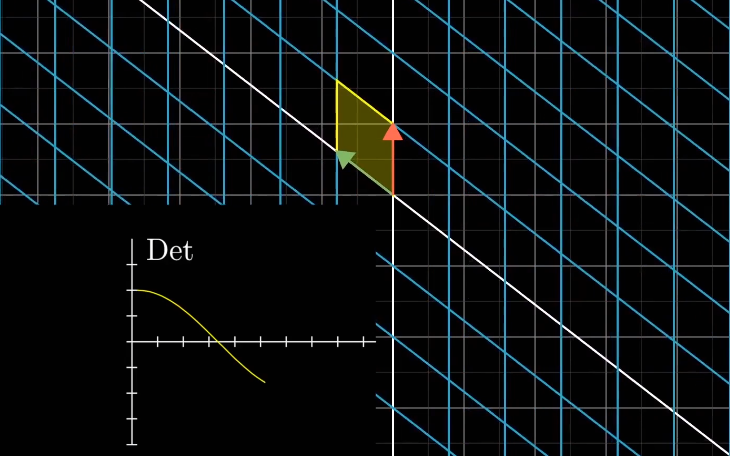
$\hat{i},\hat{j}$相互靠近时，空间被压缩。当二者重合时，$det(A)=0$ (再次表明行列式为零意味着降维)，而后继续方向“靠近”，行列式继续减小为负值似乎就是一件自然而然的事了。
det(A)从正到负
2. 矩阵的行列式（3D）
在二维空间中，行列式的值代表的是面积的缩放倍数；那么到了三维空间就代表体积的缩放倍数。
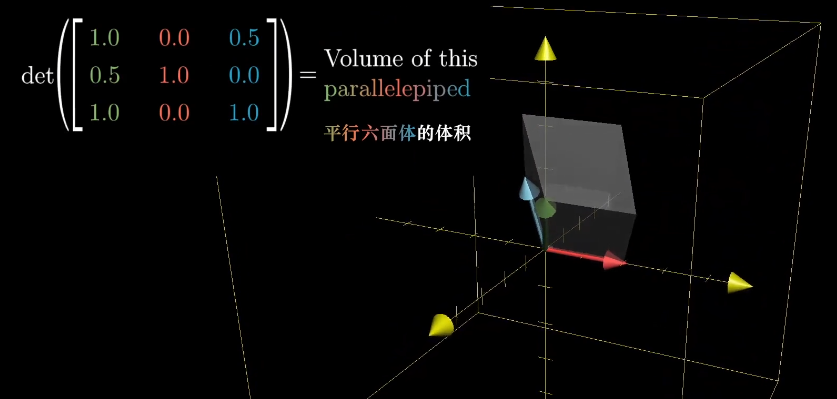
单位立方体 到平行六面体
对于三维空间中的单位立方体，经过三维线性变换后（未发生降维），它将变成一个平行六面体。其体积就是变换矩阵的行列式的（绝对）值。
变换矩阵的行列式
$det(A)=0$
同样的道理，类似于二维空间中行列式为零的情况，三维空间中变换矩阵的行列式为零（列线性相关），意味着这个变换将空间压缩到更低维度（一个面，一条线，甚至是一个点）。
$det(A)<0$
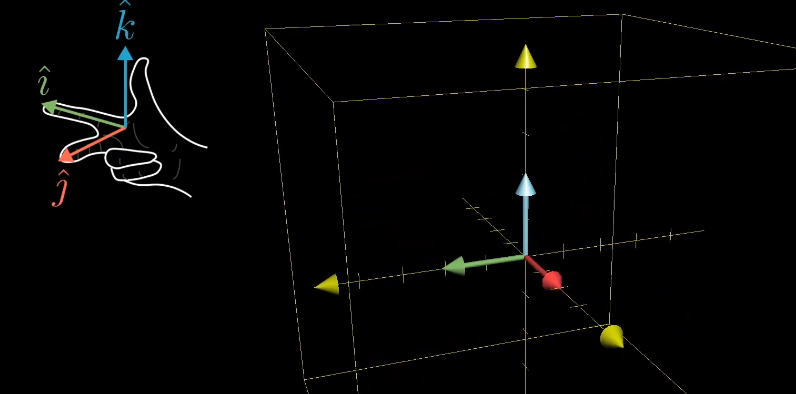
当行列式的值小于零时，我们知道这是“定向”发生了改变，这一点在三维空间中常用“右手定则”来判断，当你只能用左手来表示$\hat{i},\hat{j},\hat{k}$时，就说明“定向”发生了改变，行列式的值小于零。
右手定则示意图
3. 行列式的计算
二维空间（2D）
$$
det\left(\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}\right)=ad-bc
$$
三维空间（3D）
$$
det\left(\begin{bmatrix}
a & b & c\\
d & e & f\\
g & h & i
\end{bmatrix}\right)=a\cdot det\left(
\begin{bmatrix}
e & f\\
h & i
\end{bmatrix}\right)+b\cdot det\left(
\begin{bmatrix}
f & d\\
i & g
\end{bmatrix}
\right)+c\cdot det\left(
\begin{bmatrix}
d & e\\
g & h
\end{bmatrix}
\right)
$$
其他
$$det(M_1M_2)=det(M_1)det(M_2)$$