本文讲述的插值算法包括：最近邻插值、双线性插值及双立方插值。主要针对于二维空间（图像）的放大过程中的插值问题。

1 何为插值

  插值（Interpolation）就是一种通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。这听起来可能有些官方，你可以想象下这样一个场景：当你放大（或缩小）一幅图像时，你会怎么做？脑海里可能会有一个色块“过渡”或者说“渐变”的过程，那具体又是如何”过渡”的呢？💭

2 三种方法

  图像放大就是对原图像进行上采样的过程，涉及到从一个图像创建另一个图像。每个图像具有不同的空间几何形状。假设 $\bm I$ 是一个大小为 $R _ {in}\times C _ {in}$ 的输入图像，$\bm J$ 是一个大小为 $R _ {out}\times C _ {out}$ 的输出图像。有两种方法可以做到这一点:

• 前向映射
  • 对于输入图像 $\bm I$ 中的每一个像素 $\bm I(r,c)$，按照缩放因子映射到输出图像 $\bm J$ 中的像素 $\bm J(r’,c’)$。
• 后向映射
  • 对于输出图像 $\bm J$ 中的每一个像素 $\bm J(r,c)$，都从输入图像 $\bm I$ 中选择一个（亚）像素位置 $\bm I(r’,c’)$¹。

  很显然，第一种前向映射会导致输出图像 $\bm J$ 中的一些像素位置为空；而第二种后向映射的方法则不会产生这种问题，但是我们需要用插值法来计算“亚像素”位置的像素值。

  如同前面所假设一致，$\bm I$ 是一个大小为 $R _ {in}\times C _ {in}$ 的输入图像，我们希望将它放大到大小为 $R _ {out}\times C _ {out}$ 的输出图像 $\bm J$。则有缩放因子:

$$S _ R=\frac{R _ {out}}{R _ {in}},\quad S _ C=\frac{C _ {out}}{C _ {in}}$$

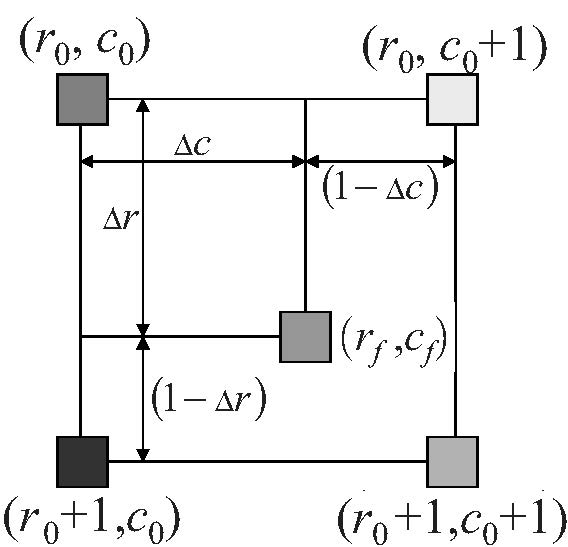
  如图2.1所示，点 $\bm I(r_f,c_f)$ 是输出图像中点 $\bm J(r,c)$ 反向映射到输入图像的点，其中 $r _ f=r/S _ R\text{，}r=1,\cdots,R _ {out}\text{，}c _ f=c/S _ C,c=1,\cdots,C _ {out}\text{，}r _ 0=\lfloor r _ f \rfloor\text{，}c _ 0=\lfloor c _ f \rfloor$.

下面是三种不同的插值方法示意图：最近邻、双线性以及双立方（2D）。

图 2.2：最近邻插值示意图	图 2.3：双线性插值示意图	图 2.4：双立方插值示意图

2.1 最近邻插值（NN）

  最近邻算法是像素复制和抽取的推广。最近邻插值算法选择距离所求数据点最近点的值，并且根本不考虑其他相邻点的值，从而产生一个分段常数的内插值来作为所求数据点的值。

  如图 2.1所示，最近邻算法就是将点 $\bm I(r_f,c_f)$ 周围4个像素点中距离最近的点作为输出图像中对应点的像素值。实际上，点 $\bm I(r_f,c_f)$ 可以是横纵坐标均小于1的点，这样周围的点中就存在横纵坐标为零的情况。为了避免这种情况同时也是一个更好的方法，我们可以将一个格子而非一个点看做是一个像素，这样像点 $(0.5,0.5)$ 一样的点都落在 $(1,1)$ 格子内，它就是距离 $(1,1)$ 最近。因此对于输出图像点 $\bm J(r,c)$ 映射到输入图像的点 $\bm I(r_f,c_f)$，我们令$\bm J(r,c)=\bm I(\lceil r_f \rceil,\lceil c_f \rceil)$。

2.2 双线性插值（Bilinear）

  双线性插值，又称为双线性内插。在数学上，双线性插值是对线性插值在二维直角网格上的扩展，用于对双变量函数（例如 $x$ 和 $y$）进行插值。其核心思想是在两个方向分别进行一次线性插值。

  如图2.1所示，$r _0=\lfloor r_f \rfloor\text{，}c_0=\lfloor c_f \rfloor\text{，}\Delta r=r_f-r_0\text{，}\Delta c=c_f-c_0$，则输出图像像素值计算公式为

  考虑到如同最近邻插值中描述的，$\bm I(r_0,c_0)$可能在矩阵中索引无效。可以考虑图像填充的方法避免或者更改索引方法。

2.3 双立方插值（Bicubic）

  在数值分析这个数学分支中，双三次插值是二维空间中最常用的插值方法。在这种方法中，函数$f$在点$(x, y)$的值可以通过矩形网格中最近的十六个采样点的加权平均得到，在这里需要使用两个多项式插值三次函数，每个方向使用一个。插值的表面比通过双线性插值或最近邻插值获得的对应表面更平滑。双三次插值可以使用Lagrange多项式，三次样条或三次卷积算法来完成。

  三次卷积算法中 $W$ 是一个三次Hermite样条曲线：

其中，$a$ 通常设置 $-0.5$ 或 $-0.75$。当 $a=-0.5$ 时，$W(x)$ 可以写作

在像素 $\bm I(r,c)$ 处，当沿列进行一维卷积时， $$d=r _ f-r,\quad I_{-1}=\bm I(r-1,c),\quad I_0=\bm I(r,c),\quad I_1=\bm I(r+1,c),\quad I_2=\bm I(r+2,c).$$ 当沿行进行卷积时， $$d=c _ f-c,\quad I_{-1}=\bm I(r,c-1),\quad I_0=\bm I(r,c),\quad I_1=\bm I(r,c+1),\quad I_2=\bm I(r,c+2).$$

如果多项式 $p$ 先按照列进行然后再进行行计算（与图2.4类似），那么输出图像像素 $\bm J(r,c)$ 就可以按照下式计算：

其中 $dr=r_f-r\text{，}dc=c_f-c$. 同样的，在双立方插值中也会有索引无效的情况，可以通过对输入图像填充解决。

3 MATLAB实现

  三种插值方法的实现都是基于MATLAB语言实现，这里给出三种方法的核心代码。

3.1 最近邻

  最近邻的实现不需要对输入图像进行填充，核心代码如下所示。

% 双重for循环
for cou1 = 1:x_new
    for cou2 = 1:y_new
        % 取最近的点，实际上用ceil更合适，而非round,同时解决了边界范围问题
        % 映射点落在哪个像素就用哪个像素，也符合最近邻的思想
        M(cou1,cou2) = I(ceil(cou1./x_scale),ceil(cou2./y_scale));
    end
end

3.2 双线性

  双线性的实现也可以不用对输入图像进行填充，实现的效果类似当输出图像反向映射到输入图像最外周时，就让这点作为输出图像的像素值。核心代码如下所示。

for cou1 = 0:x_new-1
    for cou2 = 0:y_new-1
        % 输出图像映射到输入图像的亚像素位置
        o1=cou1./x_scale;
        o2=cou2./y_scale;
        % 计算因子
        W = 1-o1+floor(o1);
        H = 1-o2+floor(o2);
        % 周围4个点
        I11 = I(1+floor(o1),1+floor(o2));
        I12 = I(1+ceil(o1),1+floor(o2));
        I21 = I(1+floor(o1),1+ceil(o2));
        I22 = I(1+ceil(o1),1+ceil(o2));
        % 计算公式
        M(cou1+1,cou2+1) = (1-W).*(1-H).*I22 + (W).*(1-H).*I21 + (1-W).*(H).*I12 + (W).*(H).*I11;
    end
end

3.3 双立方

  双立方插值的实现对输入图像进行填充，然后如节2.3所述方法计算即可，核心代码如下。

for row=1:x_new
    for column=1:y_new
        % 先沿列计算
        for m=0:3
            K(m+1)=p(dr(row),I_pad((r0(row):r0(row)+3),c0(column)+m)); 
        end
        % 再按照行计算输出像素值
        M(row,column)=p(dc(column),K);
    end
end

4 结果示例与比较

  为了比较算法实现的效果如何，本文对一系列经典图片进行测试并与MATLAB的函数imresize做了比较，主要通过计算本文实现结果和imreszie的结果的相似度来衡量实现的效果。

4.1 结果示例

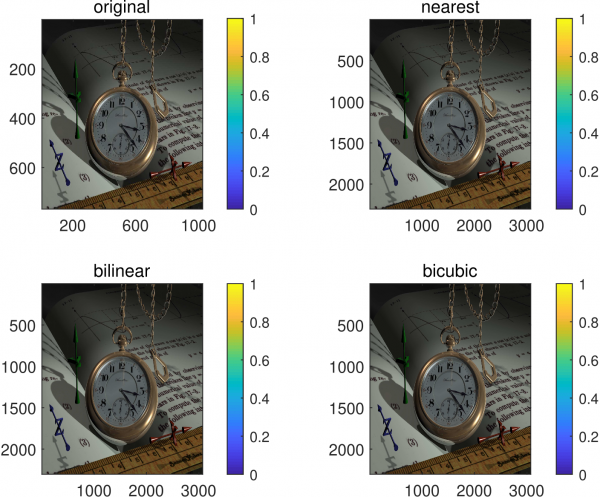
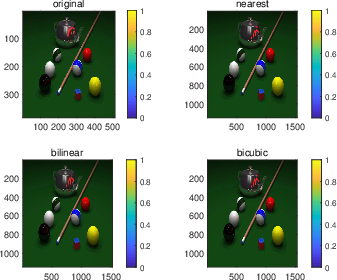
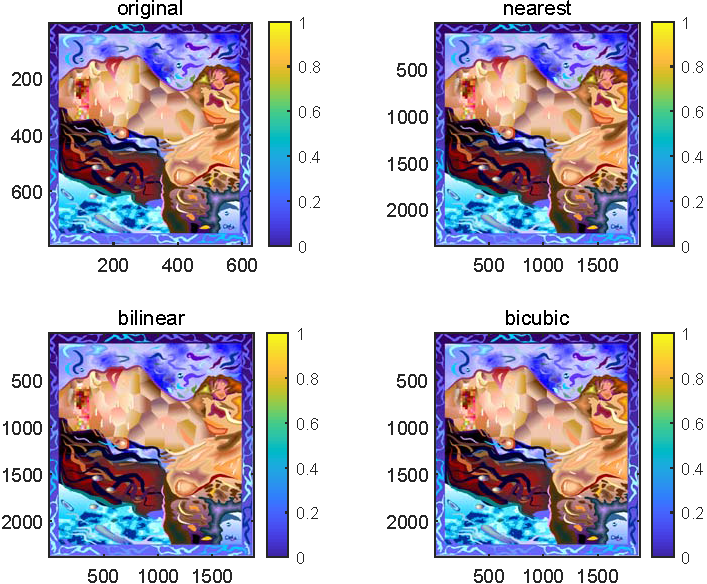
  本文只给出了部分示例结果（原始图像放大3倍），如下所示。对于此类自然图像，整体看起来三种方法效果差不多，但是看细节还是有所区别的（当然在这里是看不出来的🙃）。

图 4.1.1： Watch.png	图 4.1.2： Pool.png	图 4.1.3： Serrano.png

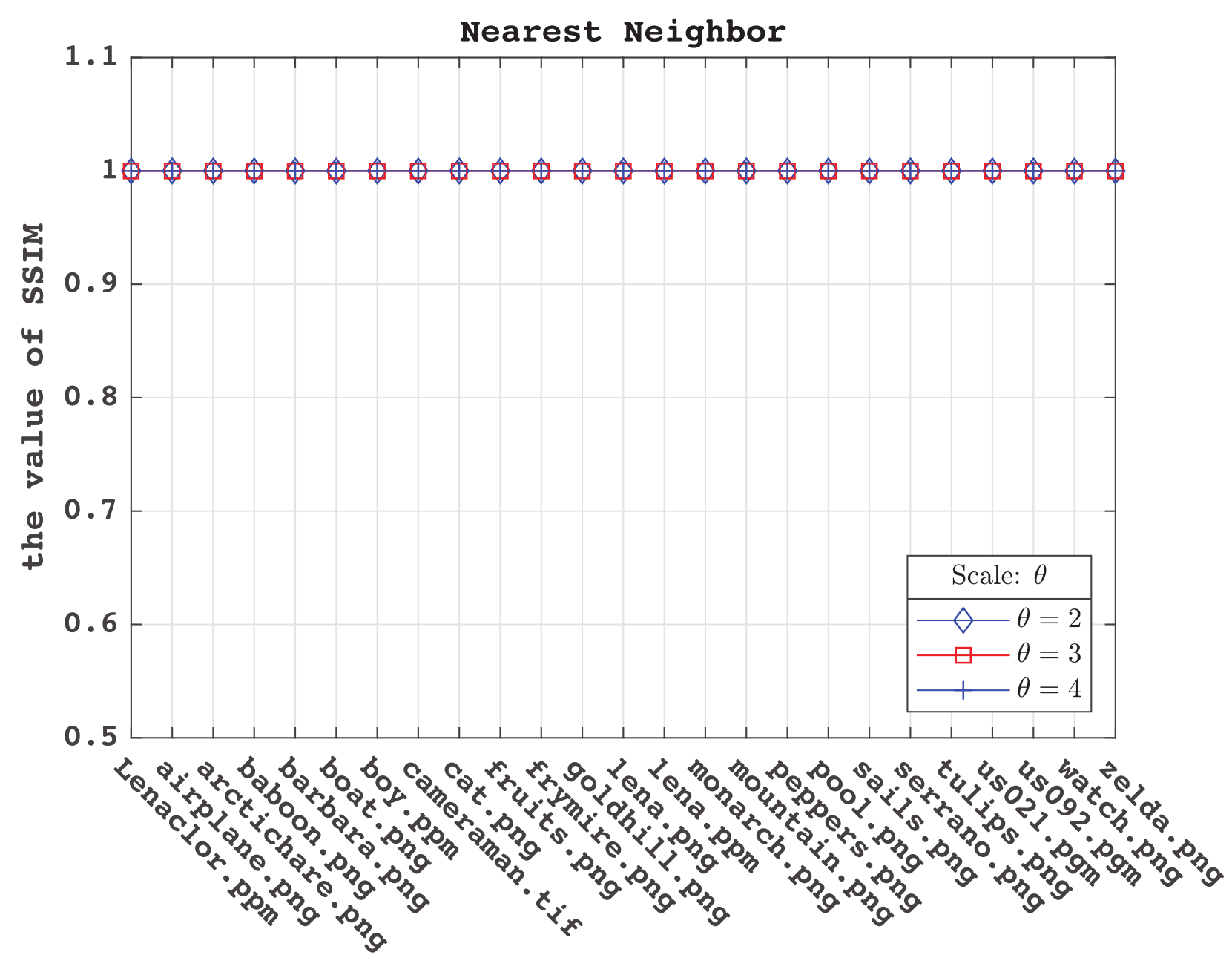
4.2 SSIM

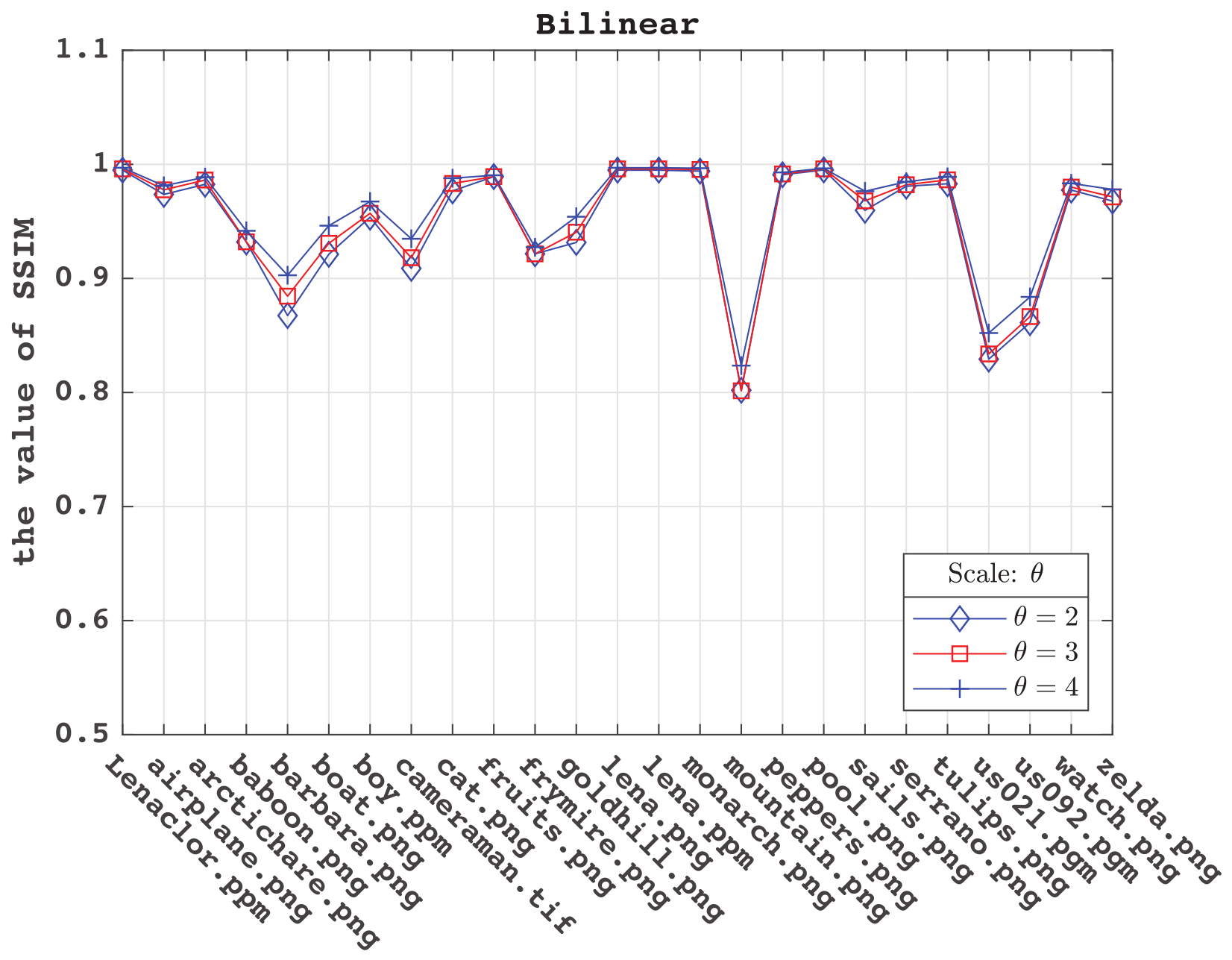
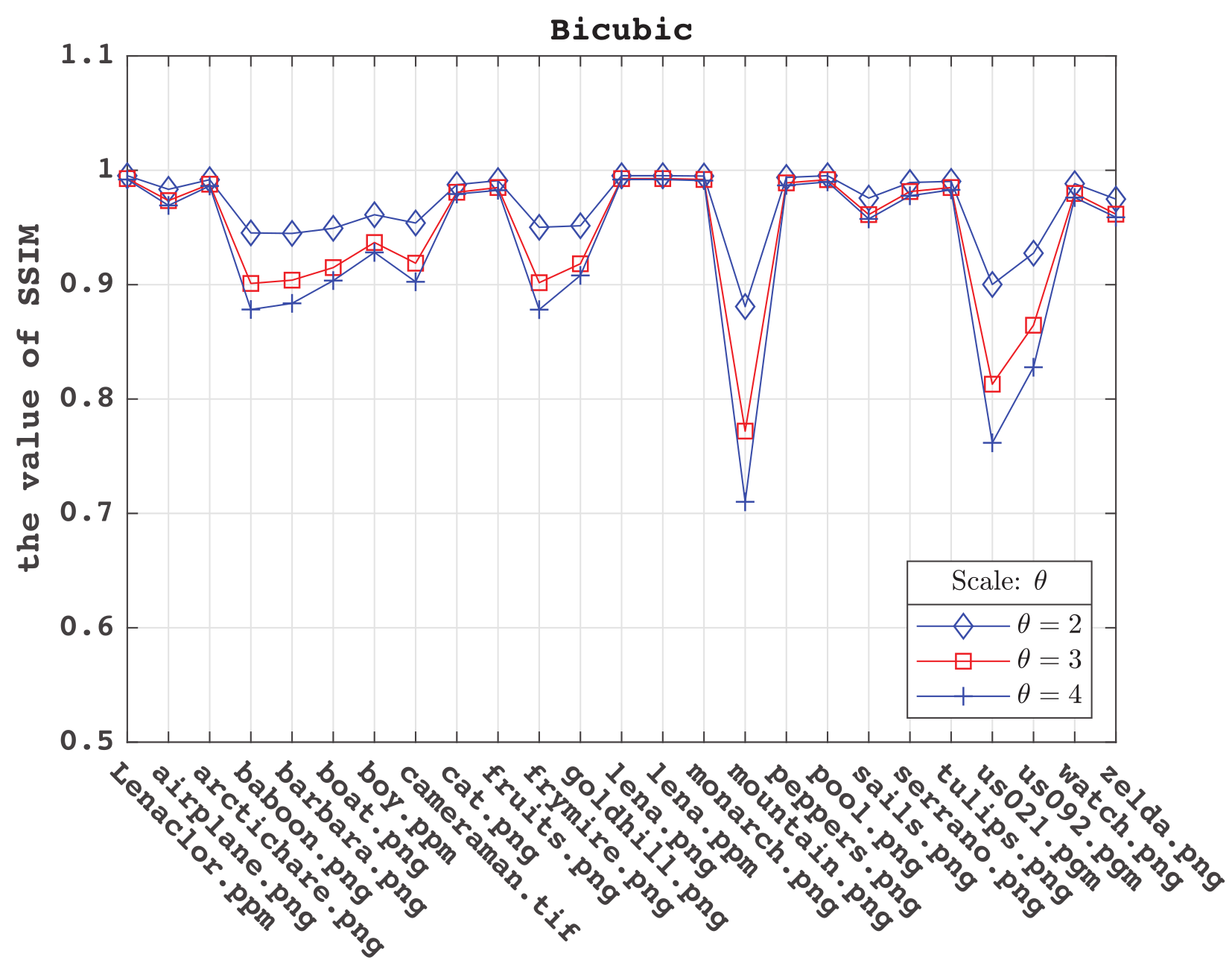
为了衡量算法实现的效果，本文将实现的结果与MATLAB的函数imresize进行了比较，三种方法比较结果如下，图中 $\theta$ 为图像放大倍数。

图 4.2.1：最近邻插值示意图	图 4.2.2：双线性插值示意图	图 4.2.3：双立方插值示意图

5 算法评价

• 就最近邻插值的实现而言，效果还不错，至少在 SSIM 值的表现上与 imresize 的结果保持着高度相似。最近邻的插值图像实则复制像素，它的的边缘更清晰，但大部分图像为块状，锯齿感较强。
• 关于双线性插值，它的实现效果与最近邻比较差点，而且在它的效果还与图片的内容有所关联。双线性插值的边缘易模糊，但大多数图像更平滑，整体看起来好。
• 双立方被认为是放大图像的最佳插值方法，MATLAB中函数imresize的默认方法也是bicubic。但本文实现的方法在放大倍数较大时程序运行耗时较长，这是一个缺点。

6 参考文献

• [1] Giassa M. Upsampling Interpolation.
• [2] EECE_4353_15_Resampling.pdf