同态滤波(Homomorphic filtering)是一种广泛用于信号和图像处理的技术，将原本的信号经由非线性映射，转换到可以使用线性滤波器的不同域，做完运算后再映射回原始域。同态的性质就是保持相关的属性不变，而同态滤波的好处是将原本复杂的运算转为效能相同但相对简单的运算。

  同态滤波利用去除乘性噪声(multiplicative noise)，可以同时增加对比度以及标准化亮度，借此达到图像增强的目的

Homomorphic filtering

  照射-反射模型可用于开发一种频率域处理过程，该过程通过同时压缩灰度级范围和增强对比度来改善一幅图像的表现，这种方法被称为同态滤波。一幅图像 $f(x,y)$ 可以表示为其照射分量 $i(x,y)$ 和反射分量 $r(x,y)$ 的乘积，即 $$ \begin{aligned} f(x,y)=i(x,y)r(x,y)\tag{1} \end{aligned} $$ 同态滤波的滤波器函数有如下形式 $$ \begin{aligned} H(u,v)=(\gamma_H-\gamma_L)[1-e^{-c(D(u,v)^2/D_0^2)}]+\gamma_L \tag{2} \end{aligned} $$ 其中，$\gamma_H>1\text{，}\gamma_L<1$，常数 $c$ 控制函数坡度的锐利度。上式中，$D_0$ 是一个正常数，$D(u,v)$ 则是频率域中点 $(u,v)$ 与频率矩形中心的距离，即

基本步骤

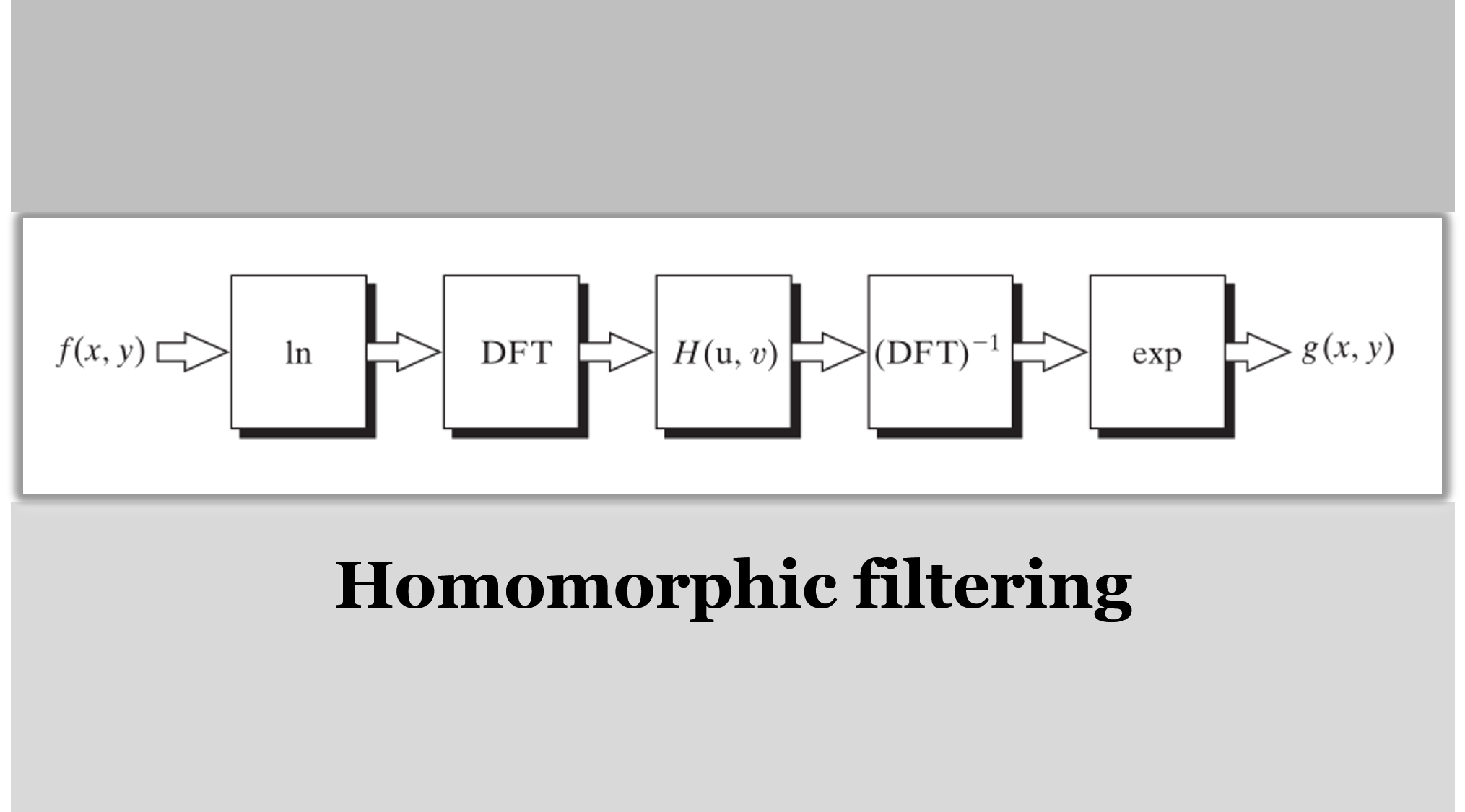
输入图像为 $f(x,y)$，同态滤波结果为 $g(x,y)$ 基本步骤如下：

STEP1: 对数变换 $z(x,y)=\ln f(x,y)=\ln i(x,y)+\ln r(x,y)$ ¹

STEP2: 傅里叶变换 $Z(u,v)=\mathfrak{F}{z(x,y)}=\mathfrak{F}{\ln f(x,y)}=\mathfrak{F}{\ln i(x,y)}+\mathfrak{F}{\ln r(x,y)}$

STEP3: 频域相乘 $S(u,v)=H(u,v)Z(u,v)$

STEP4: 傅里叶逆变换 $s(x,y)=\mathfrak{F}^{-1}{S(u,v)}$

STEP5: 指数变换 $g(x,y)=e^{s(x,y)}$

MATLAB实现

同态滤波函数homo_f如下：输入参数如式$(2)$中所述。

function Output=homo_f(I,rL,rH,c,D0)
    [M,N,C]=size(I);                % 图像矩阵维度
    P = 2*M; Q = 2*N;               % 图像填充后大小
    Output=log(double(I)+1);        % 对数变换
    D=dftuv(P,Q);                   % D(u,v)
    H=(rH-rL).*(1-exp(-c.*(D./D0^2)))+rL; % 滤波函数
    H=ifftshift(H);                 %对H做反中心化
    % 循环计算
    for i=1:C
        FI=fft2(Output(:,:,i),P,Q); %傅里叶变换 
        Ou1=ifft2(H.*FI);           %傅里叶逆变换
        Ou2 =Ou1(1:M, 1:N);         %恢复图像大小
        Ou3=exp(Ou2)-1;             %取指数
        Output(:,:,i)=Ou3;
    end
    Output=uint8(Output);
% D(u,v)计算函数，输入参数为图像大小
function D=dftuv(M,N)
    u=0:M-1;v=0:N-1;
    idx=find(u>M/2);u(idx)=u(idx)-M;
    idy=find(v>N/2);v(idy)=v(idy)-N;
    [U,V]=meshgrid(v,u);D=(U.^2+V.^2);
end
end

Reference

• [i] Gonzalez R. Digital Image Processing.

• [ii] Gonzalez R, Woods R, Eddins S. Digital Image Processing Using MATLAB.