题设
设有如下方程组:
$$
\begin{bmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\vdots&\vdots&\ddots&\vdots\\
a_{21}&a_{22}&\cdots&a_{2n}
\end{bmatrix}\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}=\begin{bmatrix}
b_1\\
b_2\\
\vdots\\
b_n
\end{bmatrix}
$$
$$
\bm\Darr
$$
$$
Ax=b
$$
求解思路
设$n$阶方阵$A$的各阶顺序主子式不为零,则存在唯一单位下三角矩阵$L$和上三角矩阵$U$使得$A=LU$。经过如下变换:
$$
Ax=b \implies LUx=b\tag{1}
$$
$$
\Darr \text{令} Ux=y
$$
$$
\begin{cases}
Ly=b\\
Ux=y
\end{cases}\tag{2}
$$
则由式$(2)$可以解得$y$,进而解得$x$.
矩阵的三角分解
设$A$为$n$阶矩阵,$L$为$n$阶下三角矩阵,$U$为$n$阶上三角矩阵。如果$A=LU$,则称对矩阵$A$实行了三角分解或者叫做$LU$分解。(注:矩阵的三角分解不唯一)
杜里特尔分解($LU$分解)
如果L为单位下三角矩阵,$U$为上三角矩阵,则称该三角分解为杜里特尔(Doolittle)分解。
分解过程
首先将分解的结果$L,U$合写在一个矩阵中,像这样:
$$
\begin{bmatrix}
u_{11} & u_{12} & u_{13} & \cdots &u_{1n}\\
l_{12} & u_{22} & u_{23} & \cdots &u_{2n}\\
l_{13} & l_{23} & u_{33} & \cdots &u_{2n}\\
\vdots&\vdots& \vdots & \ddots&\vdots\\
l_{n1} & l_{n2} & l_{n3}& \cdots &u_{nn}
\end{bmatrix}\tag{3}
$$
Doolittle分解的特点:
$\bullet$ 计算顺序:先计算$U$矩阵(即先算行,从左到右),再计算$L$矩阵(即后算列,从上到下),依次交叉进行。
$\bullet$ 计算特点:旧元素减去左边与顶上列向量的点积,计算行不用除法,计算列要除对角元。(如下图所示)
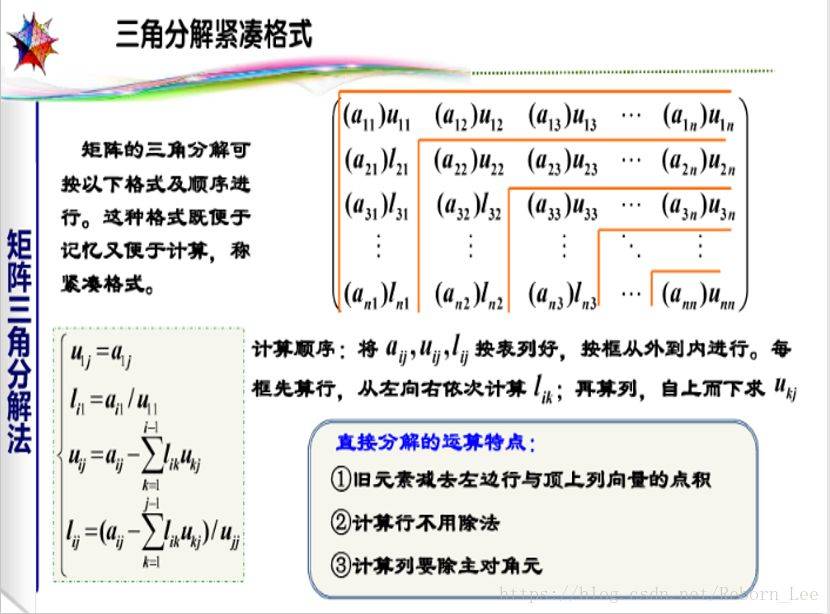
图源自水印
按照上述方法分解完成$L,U$后按照式$(2)$即可求得方程的解。
其他分解方法
还有平方根法和追赶法适用于一些特定的矩阵。其中,追赶法的分解实质上也是杜立特尔分解。
矩阵分解其他用处
矩阵分解还可以用于求矩阵的逆:
$$
A=LU \implies A^{-1}=(LU)^{-1}=U^{-1}L^{-1}\tag{4}
$$
上三角矩阵和下三角矩阵的逆较易求得。
