图像增强算法常见于对图像的亮度、对比度、饱和度、色调等进行调节，增加其清晰度，减少噪点等。由于受到环境，光线等的影响，拍摄的照片清晰度和对比度比较低，不能够突出图像中的重点。图像对比度增强就是通过一定的方法使得图像中的事物看的更清楚或更明显。本文从直方图均衡化、对数变换、幂律变换以及基于直方图统计信息进行局部增强等传统方法展开论述，展示了不同方法的实现效果并给予一定的分析。

1 方法概述

  对比度是使一个物体（或其在图像中的表示）与其他物体和背景区别开来的视觉特性的差异。在现实世界的视觉感知中，对比度是由物体和同一视场内其他物体的颜色和亮度的差异决定的。换言之，它是图像的较暗像素和较浅像素之间的区别，如果它很大，图像将具有高对比度，而在另一种情况下，图像将具有低对比度。以下是增强图像对比度的方法。

1.1 直方图均衡化

  直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法,这种方法通常用来增加图像的全局对比度。以下将从两类图像介绍该方法的实现：灰度图像、RGB真彩图。

1.1.1 灰度图像

  对于一个大小为 $M\times N$ 的灰度图像 $X$，$n_i$ 表示灰度 $i$ 出现的次数，则图像中灰度为 $i$ 的像素出现的概率为

$$ p_{x}(i)=p(x=i)=\frac{n_i}{n},\quad 0\leq i<L \tag{1} $$

其中，$L$ 是图像中所有的灰度数（通常为256），$n$ 是图像中所有的像素数，$p_x(i)$ 实际上是像素值为 $i$ 的图像的直方图，归一化到 $[0,1]$。图像的累计归一化直方图对应于 $p_x$ 的累计分布函数，可以定义为

$$ \begin{aligned} cdf_x(i)=\sum_{j=0}^{i}p_x(j)\tag{2} \end{aligned} $$

对于输入图像 $X$ 中灰度值值为 $v$ 的像素，均衡化后灰度值变化为

$$ \begin{aligned} h(v)=round\left(\frac{cdf(v)-cdf_{min}}{M\times N-cdf_{min}}\times (L-1)\tag{3}\right) \end{aligned} $$

其中，$L$ 同式 $(1)$一样，均代表灰度级数（若图像为 $l$ 位深度，则 $L=2^l$，下同）。显而易见，输入图像 $X$ 中灰度最小值和最大值将分别变化为 $0$ 和 $L-1$。

  上面描述了灰度图像上使用直方均衡化的方法，通过将这种方法分别用于图像RGB颜色值的红色、绿色和蓝色分量，从而也可以对彩色图像进行处理。但是值得注意的是，实际上对彩色分量RGB分别做均衡化，会产生奇异的点，图像不和谐。一般采用的是用HSL和HSV色彩空间进行亮度的均衡即可。

1.1.2 RGB真彩图

  直方图均衡可以被认为是图像强度的重新分布。通过将彩色图像转换为HSV/HSI图像并增强强度，同时保留色相和饱和度分量，可以实现颜色直方图均衡 。具体步骤如下：

  1. 将RGB图像转换为HSI图像
  2. 从HSI图像矩阵获取“强度矩阵”
  3. 在强度矩阵上执行直方图均衡化
  4. 使用直方图均衡的强度矩阵从HSI图像矩阵更新强度矩阵
  5. 将HSI图像转换回RGB图像

1.2 对数变换

  对数变换的通用形式为 $$ \begin{aligned} s=clog(1+r)\tag{4} \end{aligned} $$ 其中 $r$ 和 $s$ 分别代表处理前后的像素值，$c$ 为常数并假设 $r\geq 0$。该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值

1.3 幂律变换

  幂律变换的基本形式为 $$ \begin{aligned} s=cr^{\gamma}\tag{5} \end{aligned} $$ 其中 $c$ 和 $\gamma$ 为正常数。与对数变换的情况类似，部分 $\gamma$ 值得幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值

1.4 局部增强

  如节 1.1 中所述的直方图均衡化处理方法是全局化的，在某种意义上，像素基于整幅图像的灰度分布的变换函数修改。虽然这种全局方法适用于整个图像的增强，但存在这样的情况，增强图像中小区域的细节也是需要的。解决方法是以图像中每个像素的邻域中的灰度分布为基础设计变换函数。

直接从直方图获得的统计参数可以用于图像增强。令 $f(x,y)$ 表示给定图像中任意坐标 $(x,y)$ 的像素值，输入图像的平均灰度 $m$ 和灰度方差 $\sigma^2$ 分别可由式

$$ \begin{aligned} m={}&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\tag{6}\\\\ \sigma^2={}&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}[f(x,y)-m]^2 \end{aligned} $$

给出。$S _ {xy}$ 表示规定大小的以 $(x,y)$ 为中心的邻域（通常大小为 $3\times 3$），对于邻域$S _ {xy}$的局部均值以及局部方差可以根据式$(6)$得出类似的表达式。

  令 $g(x,y)$ 表示输入图像坐标 $(x,y)$ 处相应的增强后的像素值，则对于 $x=0,1,2,\cdots,M-1,y=0,1,2,\cdots,N-1$，有

$$ \begin{aligned} g(x,y)=\begin{cases} E\cdot f(x,y) &m_{S_{xy}}\leq k_0m_{G}\text{且}k_1\sigma_{G}\leq \sigma_{S_{xy}}\leq k_2\sigma_{G},\\ f(x,y)&\text{others}, \end{cases}\tag{7} \end{aligned} $$

其中，$E,k_0,k_1,k_2$ 是规定的参数；$m_G$ 是输入图像的全局均值；$\sigma _ G$ 是输入图像的标准差。参数 $m _ {S _ {xy}}$ 和 $\sigma _ {S _ {xy}}$ 分别是局部均值和标准差。$M$和$N$ 分别为图像行和列的维数 。

2 测试图片

图 2.1：测试图片

  为了更好的比较和了解以上几种图像增强方法，本文将不同的方法应用于图 2.1中的测试图片，这些图像大部分是暗色区域。由图 2.2 可以看出，这些图像的直方图中，像素多集中于灰度级暗端；可以作为图像对比度增强的测试图（对于对数变换、幂律变换以及局部增强等方法，只对图 2.1 中（a）（d）进行测试以简单说明此类方法的效果）。

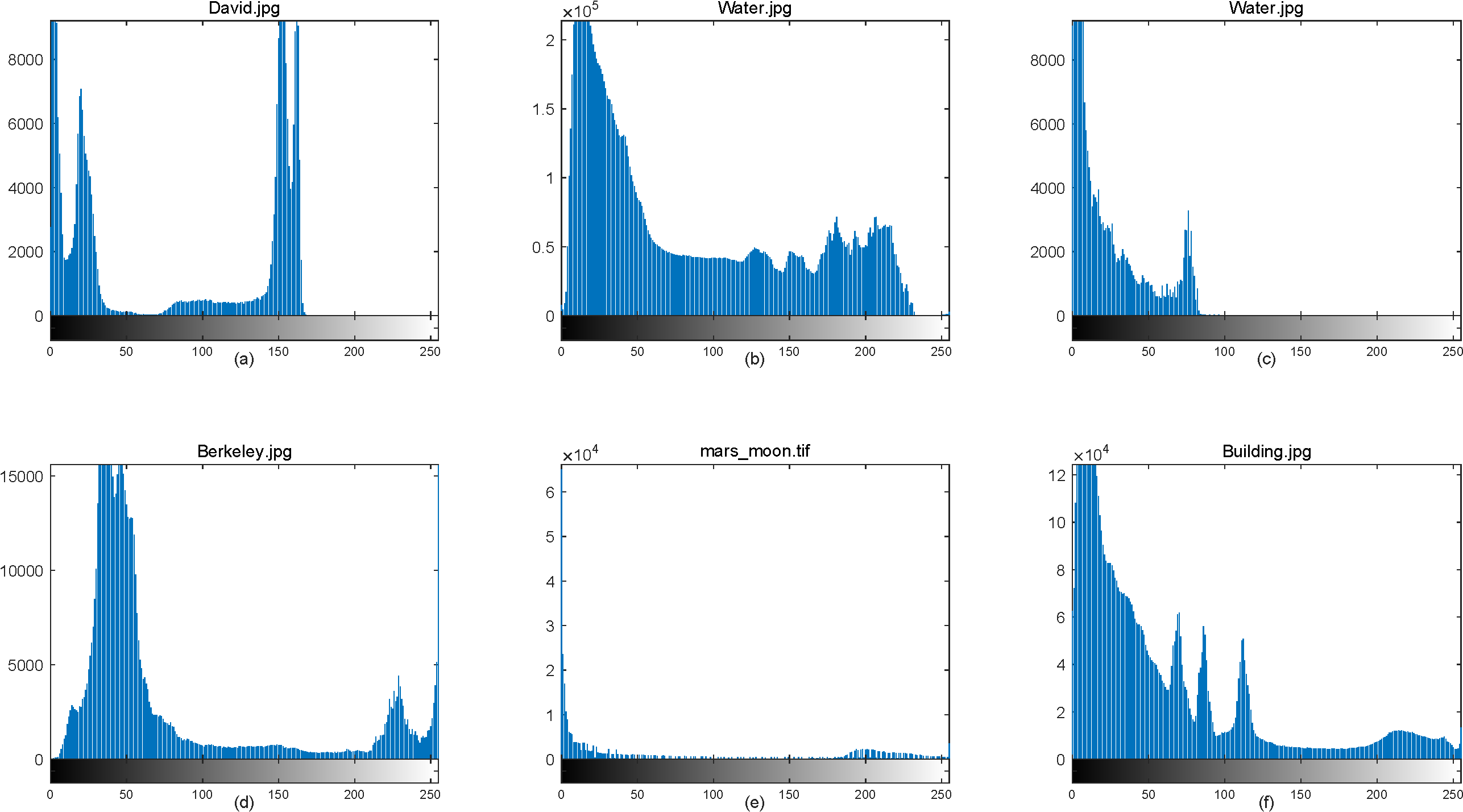
图 2.2：测试图片相应的直方图

3 测试结果

3.1 直方均衡

3.1.1 灰度图

  图 2.1 中（d）和（e）是灰度图，经过直方均衡后的结果如图 3.1所示。

图 3.1：灰度图直方图处理结果

3.1.2 RGB真彩图

  对于 RGB 图，本文使用了两种处理方法以形成对比：将节 1.1.1 的方法分别应用于RGB 的红、绿、蓝分量（简称“法 1”）以及节 1.1.2 中的色彩空间转换后的处理方法（简称“法 2”）。

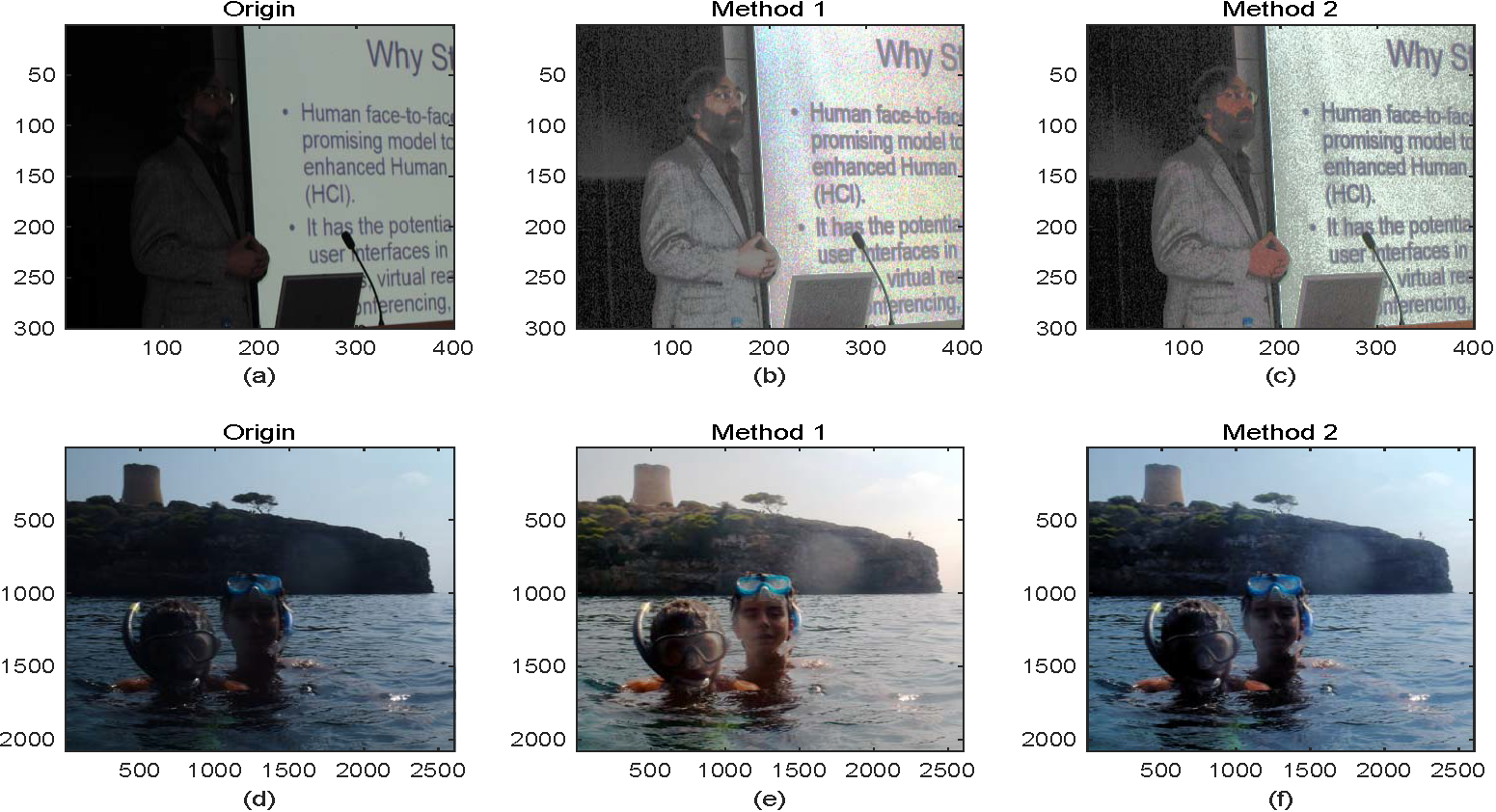
图 3.2：RGB 彩图两种方法的处理结果比照

3.2 对数变换

  如节 2 所述，只对图 2.1 中（a）（d）进行变换，处理结果如图 3.3 所示。

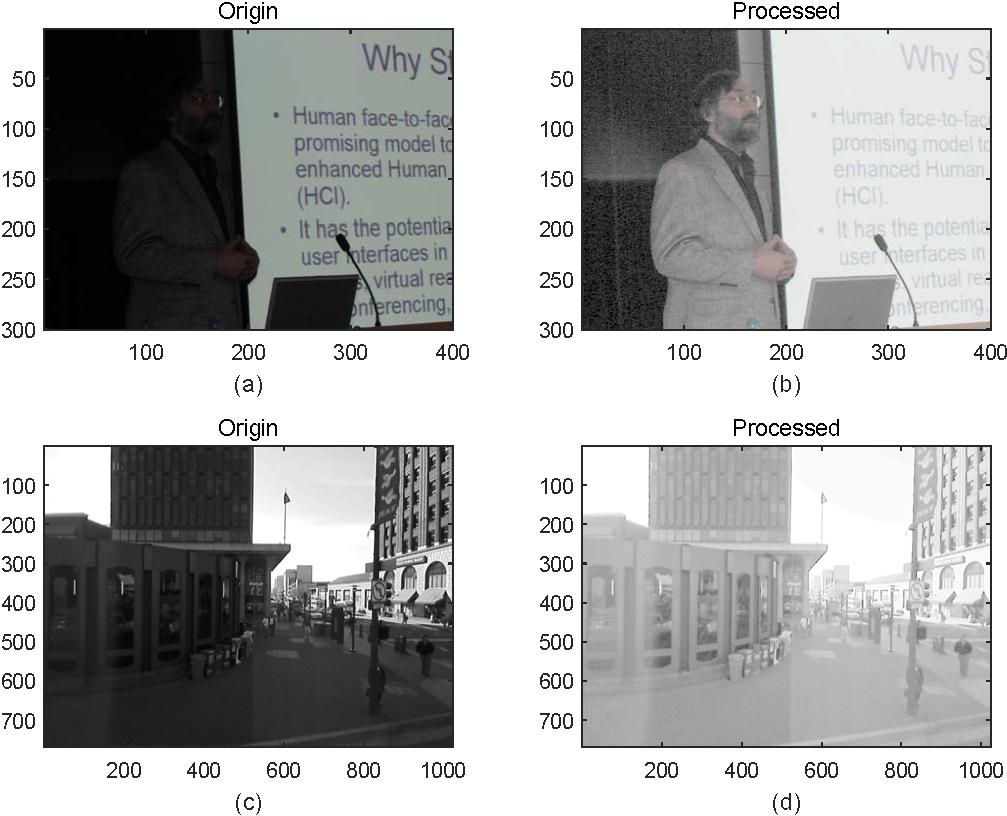
图 3.3：对数变换处理结果比照

3.3 幂律变换

  如节 2 所述，只对图 2.1 中（a）（d）进行变换，处理结果如图 3.4 所示。

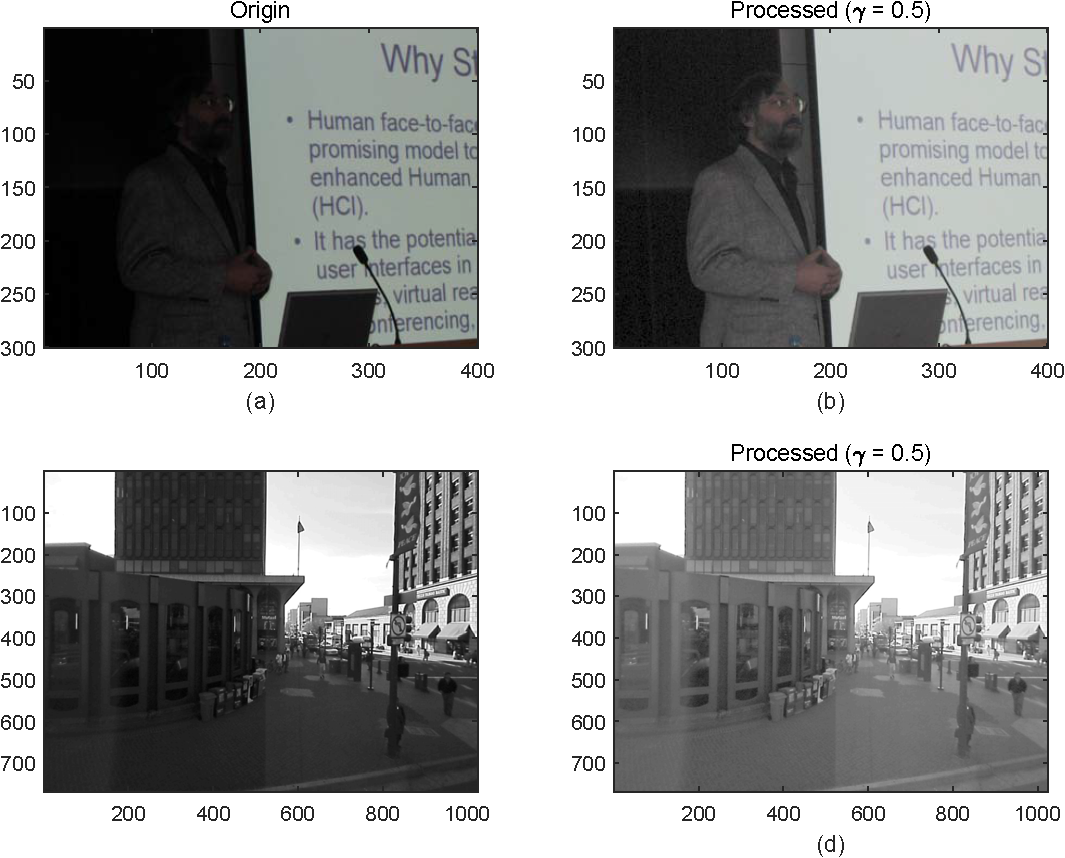
图 3.4：幂律变换处理结果比照

3.4 局部增强

  如节 2 所述，只对图 2.1 中（a）（d）进行变换，处理结果如图 3.5 所示。

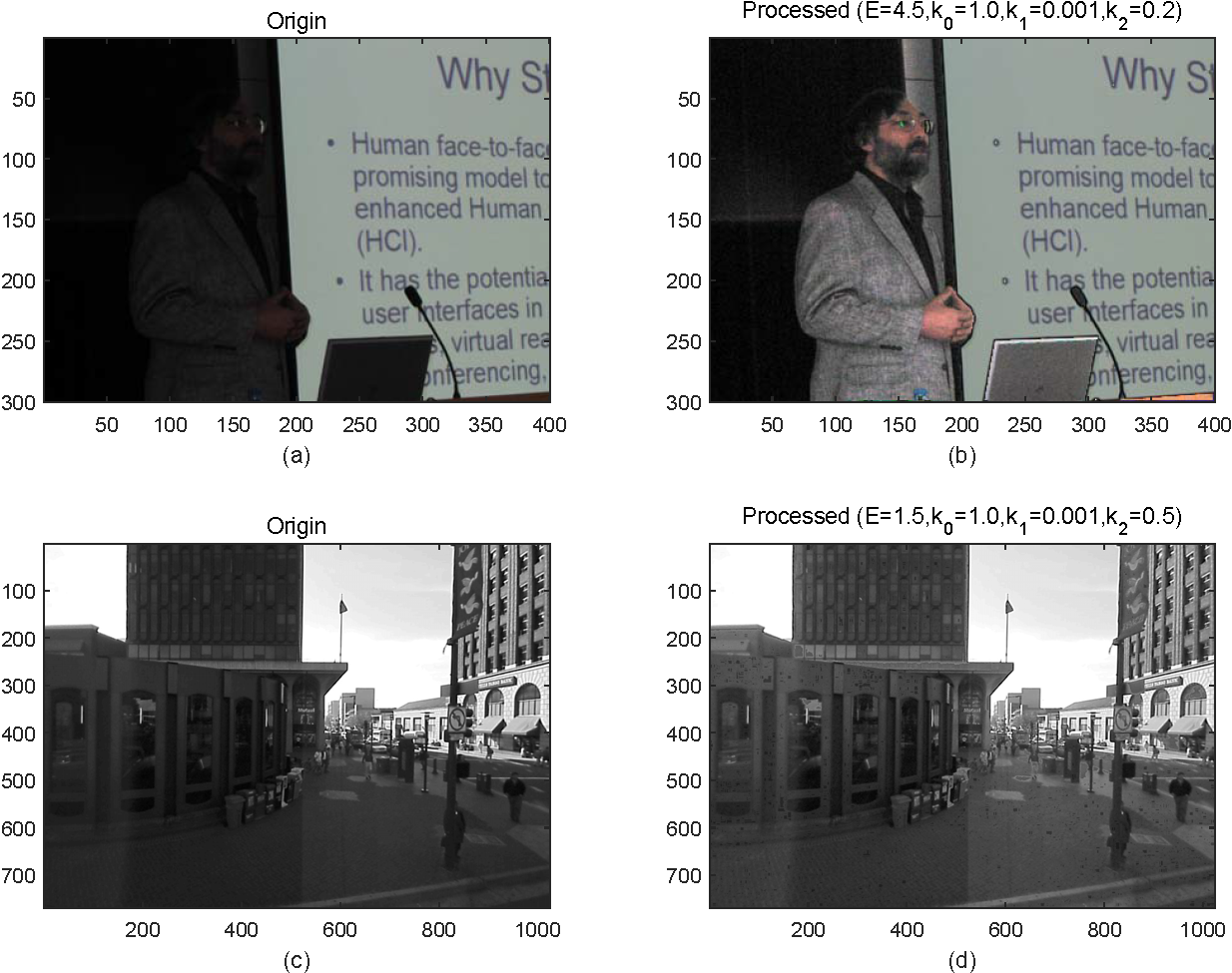
图 3.5：局部增强处理结果比照

4 结果分析

4.1 直方均衡

  • 灰度图 由图 3.1 可以看出，直方均衡对于增强对比度低或者暗的图效果还是理想的，经过直方均衡后，图像整体看起来很好。除此之外，整个直方均衡过程是自动的，对于输入的图像能够确定一个变换函数，不需要更多的参数说明。
  • RGB 真彩图 对于 RGB 真彩图，本文选择了两种方法进行直方均衡。由图 3.2 中“方法1”和“方法2”的处理结果可以看出，两种方法都能够增强图像的对比度。但是有所不同的是，直接进行三通道的直方均衡（即“方法1”）似乎使图像更“冲淡”了些。对于“方法2”，从（c、f、iii、vi）中的一些细节及整体效果可以看出，“方法2”直方均衡后的图像更加接近真实的场景。

4.2 对数变换

  对于对数变换，图像增强后的对比度高，但是整体有些过于“冲淡”。对于只对暗区域感兴趣而忽略图像的整体效果的目的，这不失为一种好的方法。

4.3 幂律变换

  对于幂律变换，不同的图所需要的参数不是很一致，在处理图像时，更多的是主观的感受来进行参数的调节。但这种方法对增强对比度，看清楚暗细节还是有一定的作用，而且这种方法处理后的整体效果也是较好的。

4.4 局部增强

  最后，对于局部增强，相较于直方图处理，比较繁琐的一点是局部增强需要不断的调整 $E,k_0 ,k_1 ,k _2$ 等参数，最终达到较好的效果。但是带来的好处是，它可以较好的保留原始图像的亮区域，对比图 3.1和 3.5中的（b，d）图可以看出。

5 MATLAB实现

5.1 直方均衡

  根据节 1.1 中的介绍，直方均衡可由如下代码实现：

%  直方均衡函数
%  若使用色彩空间转换法，则输入参数 method=2，不适用于灰度图
%  默认方法为直接循环三（或二）个通道
function Output=histe(I,varargin)
[a,b,d]=size(I);  %输入图像的维度
Output=I;
if (d==3) && (nargin>1) && (varargin==2)
    % rgb转换为hsv
    Output=rgb2hsv(I);
    % 仅强度矩阵直方均衡
    Output(:,:,3)=histeq(Output(:,:,3));
    % hsv转换为rgb输出
    Output=hsv2rgb(Output);
else
    for i=1:d
        Ic=Output(:,:,i);
        % 减少计算量
        Icc=unique(Ic);
        c=zeros(a,b);
        % 累积分布函数
        for m=1:length(Icc)
            times=find(Ic<=Icc(m));
            posi=Ic==Icc(m);
            c(posi)=length(times);
        end
        % 变换后的像素值
        c=round((c-min(c(:)))./(a*b-min(c(:))).*255);
        Output(:,:,i)=c;
    end
    Output=uint8(Output);
end
end

5.2 对数变换

  根据式$(4)$，对数变换可由如下代码简单实现：

% 对数变换函数
function Output=logg(I)
    I0=double(I);
    I0=255./log(256).*log(1+I0);
    Output=uint8(I0);
end

5.3 幂律变换

  根据式$(5)$，对数变换可由如下代码简单实现：

% 幂律变换函数
function Output=gama(I,g)
    I0=double(I);
    I0=(I0./255).^g;
    Output=uint8(I0.*255);
end

5.4 局部增强

  根据式$(6)$和$(7)$，对数变换可由如下代码简单实现：

% 局部增强函数
function I=local(I,E,k0,k1,k2)
I=double(I);
[a,b,c]=size(I);
for i=1:c
Ic=I(:,:,i);
% padding矩阵
I_pad=[zeros(1,b+2);[zeros(a,1),Ic,zeros(a,1)];zeros(1,b+2)];
% 输入图像均值及方差
mg=mean(Ic(:));
stdg=std(Ic(:));
for m=1:a
    for n=1:b
        mask=I_pad(m:m+2,n:n+2); 
        % 局部均值
        ms=mean(mask(:));
        % 局部方差
        stds=std(mask(:));
        % 满足条件则像素值乘E
        if (ms<=k0*mg)&&(stds<=k2*stdg)&&(k1*stdg<=stds)
            I(m,n,i)=E*I(m,n,i);
        end
    end
end
end
I=uint8(I);
end

6 参考文献