期末考试结束啦！终于可以有个小空写点东西了，近来复习了随机信号分析和信号系统，对一些东西有了更加深刻的认识，所以本文是自己对于如标题所列的变换的一点理解（虽然大多都是摘录的🙃），一方面也是想着忘记了还能有个东西能回顾下，主要是关于傅里叶变换及其对不同的信号（周期or非周期、离散or连续）而展开的一些变换。

1. 前言

  在信号的数学表达式中，独立变量可以是连续的，也可以是离散的。连续时间信号是定义在一个连续时间域上的，因此可以用一个连续独立变量来表示。连续时间信号常又称作模拟信号（即变量和幅值均连续）。

  离散时间信号是定义在离散时刻点上的，这样变量则具有离散值，也就是可以表示为数值的序列，因此也常称为离散时间序列。这是从变量的连续性来考量分类的，还可以根据周期性分为周期信号和非周期信号。

  为了区分连续时间和离散时间，文章内离散时间信号均称之为“序列”，另外先说两个点：

    $\bullet$ 连续时间信号和离散时间信号就是采样和重建的关系

    $\bullet$ 周期信号的周期$T\to\infty$时则转变为非周期信号

  文章的思路就是：

    $\bullet$连续时间信号部分：① 从周期信号的分解引出周期信号的频谱 ② 当周期趋于无穷时，考虑非周期信号的频谱（傅里叶变换）③ 考虑周期信号的傅里叶变换 ④ 傅里叶级数和傅里叶变换的关系

    $\bullet$离散时间序列部分：① 类比周期信号的分解推广周期序列的离散傅里叶级数（DFS） ② 当周期趋于无穷时，考虑非周期序列的频谱（离散时间傅里叶变换：DTFT）③ 有限长序列的离散傅里叶变换（DFT） ④ DTFT和DFT的区别和关系

2. 连续时间信号

2.1 周期信号的频谱

傅里叶级数：信号的分解

  两个完备的正交1函数集：三角函数集和复函数集。所谓的信号分解实质上就是将任意连续时间信号表示为一系列不同频率的正弦信号或需指数函数之和（对于周期信号）或积分（对于非周期信号）。周期信号$f(t)$可以在区间$(t_0,t_0+T)$可以展开成在完备正交信号空间中的无穷级数。两种完备集展开的无穷级数统称为“傅里叶级数”。

  $\bullet$三角函数形式

$$ \begin{aligned} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos{(n\Omega t)}+\sum_{n=1}^{\infty}b_n\sin{(n\Omega t)}\\ &=\frac{A_0}{2}+\sum_{n=1}^{\infty}A_n\cos{(n\Omega t+\varphi_n)}\tag{1} \end{aligned} $$

式中，$\Omega=2\pi F=2\pi /T$为角频率；$a_n,b_n$则称为傅里叶系数且有如下计算公式：

$$ a _ { n } = \frac { 2 } { T } \int _ { - \frac { T } { 2 } } ^ { \frac { T } { 2 } } f ( t ) \cos ( n \Omega t ) d t , \quad n = 0,1,2,\cdots\tag{2} $$ $$ b _ { n } = \frac { 2 } { T } \int _ { - \frac { T } { 2 } } ^ { \frac { T} { 2 } } f ( t ) \sin ( n \Omega t ) d t , \quad n = 1,2,\cdots\tag{3} $$

  $\bullet$指数形式

  三角函数形式的傅里叶级数含义比较明确，但是计算不便，因此可以利用欧拉公式和傅里叶系数的性质2将其变形为指数形式的傅里叶级数。

$$ f(t)=\sum_{-\infty}^{\infty} A_ne^{j\varphi_n} e^{jn\Omega t}=\sum _ {-\infty}^{\infty}F _ ne^{in\Omega t}\tag{4} $$

$$ F_n=\frac{1}{T}\int _{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt,\quad n=0,\pm 1, \pm 2,\cdots\tag{5} $$

周期信号的频谱

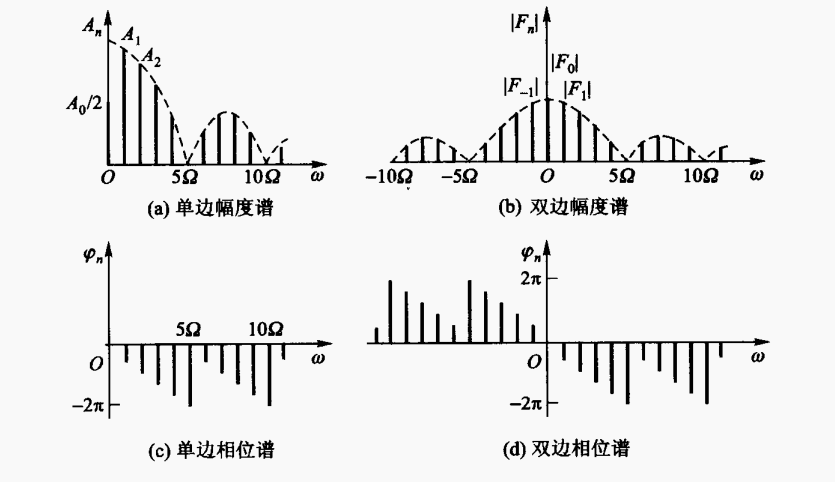
  如前所述，周期信号可以分解为一系列频率不同的信号分量（各次谐波）的组合，为了直观表示出这些分量的振幅，以频率（或角频率）为横坐标，以各谐波的振幅$A_n$或虚指数函数的幅度$|F_n|$为纵坐标，可画出下图所示的线图，称为幅度频谱，简称幅度谱。

周期信号的频谱

  从图中也可以看出，周期信号的频谱是离散谱，谱间隔就是基波频率$\Omega=2\pi /T$，那么当周期信号的周期$T\to\infty$时，变为非周期信号，相邻谱线间隔减小到零，周期信号的离散频谱就变成了非周期信号的连续谱。这就是接下来一部分要细说的：从周期信号到非周期信号。

2.2 非周期信号的频谱

傅里叶变换（FT）

  如前所述，当周期T趋近于无限大时，相邻谱线的间隔$\Omega$趋近于无穷小，从而信号的频谱密集成为连续频谱。同时，各频率分量的幅度也都趋近于无穷小，不过，这些无穷小量之间仍保持一定的比例关系。为了描述非周期信号的频谱特性,引人频谱密度的概念。令

$$ F(jw)=\lim _ {T\to \infty}\frac{F _n}{1/T}=\lim _ {T\to\infty}F _ nT\tag{6} $$

称$F(jw)$为频率谱密度函数。

  当周期$T\to\infty$时，$\Omega\to(-\infty)$，取其为$dw$，而$1/T=\Omega/2\pi$将趋近于$dw/2\pi$，$n\Omega$是变量，当$\Omega\neq 0$时，它是离散值，当$\Omega$趋于无穷小时，它就变成连续变量，取为$w$，同时求和符号改为积分。由式$(4)$和$(5)$可得傅里叶变换对如下：

$$ \begin{aligned} F ( j \omega ) & = \int_ {-\infty } ^ { \infty }f(t) e ^ { - jwt } dt \\ f ( t ) & = \frac { 1 } { 2 \pi } \int _ { - \infty } ^ { \infty } F ( j \omega ) e ^ { j \omega t } d \omega\tag{7} \end{aligned} $$

  时间函数（信号）$f(t)$可以用频谱函数（频谱密度）$F(jw)$表示。信号的两种描述方法：时域、频域。

2.3 周期信号的傅里叶变换

  一句话概括就是：周期信号的傅里叶变换（频谱密度）由无穷多个冲激函数组成，这些冲激函数位于信号的各次谐波（$n\Omega$）处，且强度为各相应幅度$F_n$的$2\pi$倍。

两种方法推导

  $\bullet$ 傅里叶变换的性质（频移特性）

$$ f_{T}(t)=\sum_{n=-\infty}^{\infty}F_ne^{jwt}\tag{8} $$ $$ \bm\Darr $$ $$ \mathscr{F}[f_{T}(t)]=2\pi\sum_{n=-\infty}^{\infty}F_n\delta(w-n\Omega)\tag{9} $$

  $\bullet$ 周期信号可以看做是信号的单个周期卷积单位周期卷积冲激序列$\delta_{T}(t)$

$$ f_{T}(t)=f_0(t)*\delta(t)\tag{10} $$ $$ \bm\Darr $$ $$ \mathscr{F}[f_{T}(t)]=\Omega\sum_{n=-\infty}^{\infty}F_0(jn\Omega)\delta(w-n\Omega)\tag{11} $$

2.4 傅里叶系数和傅里叶变换

  由式$(9)$和$(11)$可以得出如下关系：

$$ F_n=\frac{1}{T}F_0(jn\Omega)=\frac{1}{T}F_0(jw)|_{w=n\Omega}\tag{12} $$

即周期信号的傅里叶系数$F_n$等于$F_0(jw)$在频率为$n\Omega$处的值乘以$1/T$.

3. 离散时间序列

  将傅里叶级数和傅里叶变换应用到离散时间序列称为序列的傅里叶分析，它对于信号分析和处理技术的实现具有重要的意义。

3.1 周期序列

  具有周期性的离散时间信号可以额表示为$f_N(k)$，其下标$N$表示其周期为$N$，即有

$$ f_N(k)=f_N(k+LN)\quad (l\text{为任意整数}) $$

离散傅里叶级数（DFS）

  对于连续时间信号，周期信号$F_T(t)$可以分解为一系列角频率为$n\Omega(n=0,\pm 1,\pm 2,\cdots$的虚指数$e^{jwt}$（其中$\Omega=2\pi/T$是基波角频率）之和。类似的，周期为$N$的序列$f_N(k)$也可以展开为许多虚指数$e^{jn\Omega k}=e^{jn\frac{2\pi}{N}k}$（其中$\Omega=2\pi/T$是基波数字角频率）之和。

  值得注意的是，周期信号的傅里叶级数和周期序列的有所不同。虚指数序列满足

$$ e^{jn\frac{2\pi}{N}k}=e^{j(n+lN)\frac{2\pi}{N}k}\tag{13} $$

即它也是周期为$N$的周期序列。因此周期序列的傅里叶级数展开式仅为有限项（$N$项）。

  若取第一个周期$n=0,1,2,\cdots,N-1$，则$f_N(k)$展开式可以写为

$$ f_N(k)=\frac{1}{N}\sum_{n=0}^{N-1}F_N(n)e^{jn\Omega k}\tag{14} $$

$DFS[\cdot]$表示求离散傅里叶级数（正变换），以$IDFS[\cdot]$表示求离散傅里叶级数展开式（逆变换），则有

$$ \begin{aligned} DFS[f_N(k)]& =F_N(n)=\sum_{k=0}^{N-1}f_N(k)e^{-jn\Omega k}\\ IDFS[F_N(n)]&= f_N(k)=\frac{1}{N}\sum_{n=0}^{N-1}F_N(n)e^{jn\Omega k}\tag{15} \end{aligned} $$

3.2 非周期序列

离散时间傅里叶变换（DTFT）

  与连续时间信号类似，当周期序列的周期趋近于无穷大时，周期序列变为非周期序列。同时谱线间隔趋近于无穷小，成为连续谱。

  当$N\to\infty$时，$n\Omega=2\pi n/N$趋近于连续变量$\theta$（数字角频率，单位为rad），式$(15)$是在一个周期内求和，可以扩展为$(-\infty,\infty)$，则得非周期序列$f(k)$的离散时间傅里叶变换（DTFT)为

$$ \begin{aligned} F(e^{j\theta})&=\lim_{N\to\infty}\sum_{k=\lt N\gt}f_{N}(k) e^{-jn\frac{2\pi}{N}k}\\ &=\sum_{-\infty}^{\infty}f(k)e^{-jk\theta}=|F(e^{j\theta)}| e^{j\varphi(\theta)}\tag{16} \end{aligned} $$

可见，非周期序列的离散时间傅里叶变换$F(e^{j\theta})$是$\theta$的连续周期函数，周期为$2\pi$。非周期序列的离散时间傅里叶逆变换为

$$ f(k)=\frac{1}{2\pi}\int_{-\pi}^{\pi}F(e^{j\theta})e^{j\theta k}d\theta\tag{17} $$

离散傅里叶变换（DFT）

  离散傅里叶变换（DFT）的定义是为了便于实现计算机实现，它是借助离散傅里叶级数的概念，把有限长序列作为周期性离散信号的一个周期来处理。

  设有限长序列的长度为$N$（在$0\leq k\leq N-1$范围内），则$f(k)$离散傅里叶变换和逆变换定义分别为

$$ \begin{aligned} F(n)&=DFT[f(k)]=\sum_{k=0}^{N-1}f(k)e^{-j\frac{2\pi}{N}kn}=\sum_{k=0}^{N-1}f(k)W^{kn}\quad (0\leq n\leq N-1)\\ f(k)& =IDFT[F(n)]=\frac{1}{N}\sum_{n=0}^{N-1}F(n)e^{j\frac{2\pi}{N}kn}=\frac{1}{N}\sum_{n=0}^{N-1}F(n)W^{-kn}\quad (0\leq k \leq N-1)\tag{18} \end{aligned} $$

DTFT与DFT的联系

  有限长序列$f(k)$的离散傅里叶变换$F(n)$与其离散时间傅里叶变换$F(e^{j\theta}$的关系如下：由式$(16)$得DTFT为：

$$ F(e^{j\theta})=\sum_{k=-\infty}^{\infty}f(k)e^{-j\theta k}=\sum_{k=0}^{N-1}f(k)e^{-j\theta k}\tag{19} $$

对比式$(18)$中的DFT结果$F(n)$可得

$$ F(n)=F(e^{j\theta})|_{\theta=\frac{2\pi}{N}}\tag{20} $$

结果表明：$F(n)$是对$F(e^{j\theta})$在$2\pi$周期内进行$N$次均匀取样的结果。

相关文章推荐


  1. 定义在区间$(t_1,t_2)$的两个函数$\varphi_1(t)$和$\varphi _ 2(t)$，若满足$\int_{t _ 1}^{t _ 2}\varphi _ 1(t)\varphi _2(t)dt=0$，则称$\varphi _ 1(t),\varphi _ 2(t)$在区间. [return]
  2. $A_n=A _ {-n},\varphi _ {-n}=-\varphi _ n$ [return]